Optional clients¶

In this short tutorial we introduce optional clients which offer a reward (a prize) when they are serviced on a route, but whose service is not required for feasibility. This routing variant is often called a prize-collecting vehicle routing problem, and PyVRP supports this out-of-the-box.

[1]:

import pyvrp
import pyvrp.plotting
import pyvrp.stop

We will set different prize values for different clients. This can be used to reflect different service priorities.

[2]:

COORDS = [(456, 320), (312, 418), (114, 80), (570, 160), (684, 240)]
PRIZES = [500, 300, 500, 300]

[3]:

m = pyvrp.Model()

m.add_depot(x=COORDS[0][0], y=COORDS[0][1])
m.add_vehicle_type(1)

for idx in range(1, len(COORDS)):
    m.add_client(
        x=COORDS[idx][0],
        y=COORDS[idx][1],
        prize=PRIZES[idx - 1],
        required=False,
    )

for frm in m.locations:
    for to in m.locations:
        distance = abs(frm.x - to.x) + abs(frm.y - to.y)
        m.add_edge(frm, to, distance=distance)

res = m.solve(stop=pyvrp.stop.MaxRuntime(1))

PyVRP v0.14.0a0

Solving an instance with:
    1 depot
    4 clients
    1 vehicle (1 vehicle type)

    Iters    Time |      Current OK    Candidate OK         Best OK

Search terminated in 1.00s after 51962 iterations.
Best-found solution has cost 1560.

Solution results
================
    # routes: 1
     # trips: 1
   # clients: 3
   objective: 1560
    distance: 1260
    duration: 0
# iterations: 51962
    run-time: 1.00 seconds

PyVRP quickly finds a solution visiting three clients. Since the instance has four clients, one client is unvisited. Let’s visually investigate why:

[4]:

pyvrp.plotting.plot_solution(res.best, m.data(), plot_clients=True)

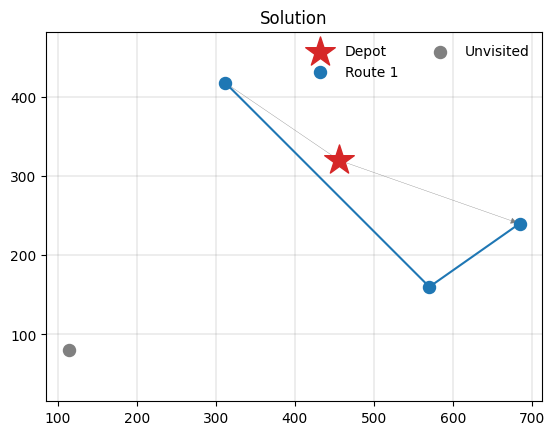
The three visited clients are all close to the depot, but the one unvisited client is not. That’s why PyVRP has decided not to service that client: the prize value is not sufficiently high to warrant a detour.

We can incentivise PyVRP to service this client by setting a higher prize, or enforce service by making the visit required. Let’s try to increase the prize, and solve the model again:

[5]:

PRIZES[1] = 1_000

[6]:

m = pyvrp.Model()

m.add_depot(x=COORDS[0][0], y=COORDS[0][1])
m.add_vehicle_type(1)

for idx in range(1, len(COORDS)):
    m.add_client(
        x=COORDS[idx][0],
        y=COORDS[idx][1],
        prize=PRIZES[idx - 1],
        required=False,
    )

for frm in m.locations:
    for to in m.locations:
        distance = abs(frm.x - to.x) + abs(frm.y - to.y)
        m.add_edge(frm, to, distance=distance)

res = m.solve(stop=pyvrp.stop.MaxRuntime(1))

PyVRP v0.14.0a0

Solving an instance with:
    1 depot
    4 clients
    1 vehicle (1 vehicle type)

    Iters    Time |      Current OK    Candidate OK         Best OK

Search terminated in 1.00s after 48559 iterations.
Best-found solution has cost 1816.

Solution results
================
    # routes: 1
     # trips: 1
   # clients: 4
   objective: 1816
    distance: 1816
    duration: 0
# iterations: 48559
    run-time: 1.00 seconds

With the prize increase, visiting all clients is now worthwhile:

[7]:

pyvrp.plotting.plot_solution(res.best, m.data(), plot_clients=True)

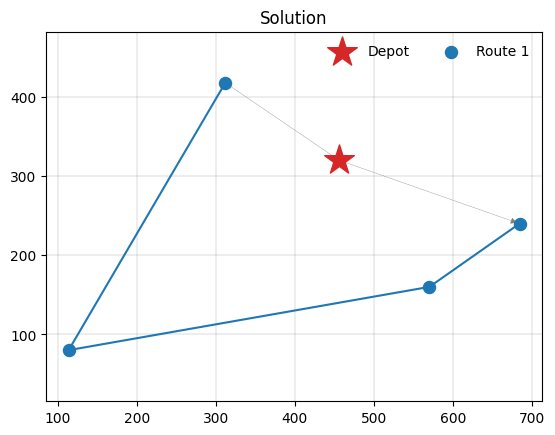
Conclusion¶

In this tutorial you have learned about modelling optional clients using PyVRP, and incentivising the solver to visit optional clients using the client’s prize attribute. Optional clients are very helpful to ensure a feasible solution is always obtained, even when there are constraints that prevent PyVRP from servicing all clients. Furthermore, different prizes can be used to model different visit priorities: all else equal, PyVRP will prefer to schedule a higher-prize visit over one where it collects a lower prize.