Modelling with PyVRP¶

This quickstart notebook is intended as a first entrypoint to working with PyVRP. We will model and solve several vehicle routing problems, using PyVRP’s high level Model interface. This interface makes it easy to define routing problems directly, using familiar routing terminology of clients, depots, vehicle types, and edges.

We start by modelling the routing problem of a small delivery company with a single depot and a few clients. As the business grows and constraints become more realistic, we adapt our model step-by-step. After the quickstart, you will be able to solve routing problems using PyVRP and are ready for the more focused tutorials presented elsewhere in our documentation.

Starting small¶

Our delivery company starts simple: initially it just wants to deliver a number of boxes to each client to meet the client demand. The boxes are stored at the company’s depot. It has two vehicles available to deliver the boxes with, and each vehicle can carry twenty boxes.

[1]:

import pyvrp
import pyvrp.plotting
import pyvrp.stop

[2]:

DEPOT_COORDINATES = (51.0, 51.0)
COORDINATES = [(39, 76.5), (64.2, 47), (73, 61), (32, 38.8)]
DEMANDS = [5, 3, 7, 2]

Using the COORDINATES and DEMANDS above for all locations, we can specify and solve a simple model as follows. We will use simplified Manhattan distances for the examples. Normally, distances (and durations) need to be obtained using real-world map data, but that is outside the scope of this example.

[3]:

m = pyvrp.Model()

depot = m.add_depot(
    x=DEPOT_COORDINATES[0],
    y=DEPOT_COORDINATES[1],
    name="Depot",
)

vehicles = m.add_vehicle_type(num_available=2, capacity=20)

for idx in range(len(COORDINATES)):
    m.add_client(
        x=COORDINATES[idx][0],
        y=COORDINATES[idx][1],
        delivery=DEMANDS[idx],
        name=f"Client {idx + 1}",
    )

for frm in m.locations:
    for to in m.locations:
        dist = int(abs(frm.x - to.x) + abs(frm.y - to.y))
        m.add_edge(frm, to, distance=dist)

res = m.solve(stop=pyvrp.stop.MaxRuntime(1))  # one second of runtime

PyVRP v0.14.0a0

Solving an instance with:
    1 depot
    4 clients
    2 vehicles (1 vehicle type)

    Iters    Time |      Current OK    Candidate OK         Best OK

Search terminated in 1.00s after 41472 iterations.
Best-found solution has cost 163.

Solution results
================
    # routes: 1
     # trips: 1
   # clients: 4
   objective: 163
    distance: 163
    duration: 0
# iterations: 41472
    run-time: 1.00 seconds

We have quickly obtained a solution to this small problem. PyVRP recommends using a single vehicle:

[4]:

for idx, route in enumerate(res.best.routes()):
    print(f"Route #{idx}:")

    for visit in route.schedule():
        loc = m.locations[visit.location]
        print(f" - At {loc}.")

Route #0:
 - At Depot.
 - At Client 4.
 - At Client 1.
 - At Client 3.
 - At Client 2.
 - At Depot.

PyVRP provides much more information about routes, schedules, and visits. We will investigate that later, once we take into account travel duration and associated constraints. For now, let’s first explore what these routes look like visually:

[5]:

pyvrp.plotting.plot_solution(res.best, m.data())

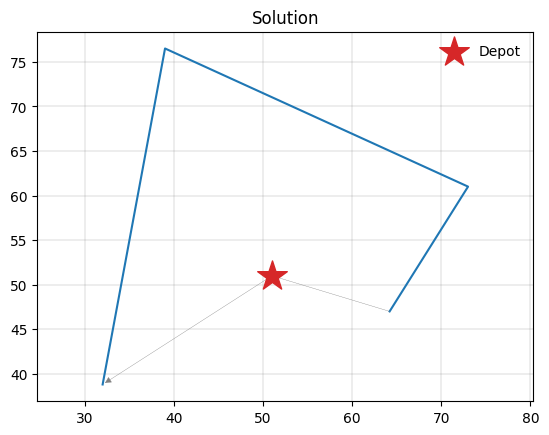
We have succesfully solved our first, simple routing problem: the delivery company now knows what to do.

Improving client and driver satisfaction¶

Some time later, the company again approaches us. To improve client satisfaction, the business has agreed to deliver during specific time windows. Further, the drivers were unhappy with long shifts, and demand that they only work a maximum shift duration.

To adhere to these new business constraints, we need to update our simple model to include TIME_WINDOWS and a SHIFT_DURATION.

[6]:

TIME_WINDOWS = [(0, 60), (60, 120), (0, 60), (60, 120)]
SHIFT_DURATION = 120

We need to update our model to account for the time windows and vehicle shift duration. That suffices to model the new business constraints.

[7]:

m = pyvrp.Model()

depot = m.add_depot(
    x=DEPOT_COORDINATES[0],
    y=DEPOT_COORDINATES[1],
    name="Depot",
)

vehicles = m.add_vehicle_type(
    num_available=2,
    capacity=20,
    shift_duration=SHIFT_DURATION,
)

for idx in range(len(COORDINATES)):
    m.add_client(
        x=COORDINATES[idx][0],
        y=COORDINATES[idx][1],
        delivery=DEMANDS[idx],
        tw_early=TIME_WINDOWS[idx][0],
        tw_late=TIME_WINDOWS[idx][1],
        name=f"Client {idx + 1}",
    )

for frm in m.locations:
    for to in m.locations:
        dist = int(abs(frm.x - to.x) + abs(frm.y - to.y))
        m.add_edge(frm, to, distance=dist, duration=dist)

res = m.solve(stop=pyvrp.stop.MaxRuntime(1))  # one second of runtime

PyVRP v0.14.0a0

Solving an instance with:
    1 depot
    4 clients
    2 vehicles (1 vehicle type)

    Iters    Time |      Current OK    Candidate OK         Best OK

Search terminated in 1.00s after 35629 iterations.
Best-found solution has cost 183.

Solution results
================
    # routes: 2
     # trips: 2
   # clients: 4
   objective: 183
    distance: 183
    duration: 183
# iterations: 35629
    run-time: 1.00 seconds

PyVRP found a new solution, this time using both vehicles to spread the work. Let’s investigate the route plan:

[8]:

for idx, route in enumerate(res.best.routes()):
    print(f"Route #{idx} [duration = {route.duration()}]:")

    for visit in route.schedule():
        loc = m.locations[visit.location]
        print(f" - [t = {visit.start_service:>03}] At {loc}.")

Route #0 [duration = 71]:
 - [t = 006] At Depot.
 - [t = 038] At Client 3.
 - [t = 060] At Client 2.
 - [t = 077] At Depot.
Route #1 [duration = 112]:
 - [t = 000] At Depot.
 - [t = 037] At Client 1.
 - [t = 081] At Client 4.
 - [t = 112] At Depot.

These routes respect the client time windows, as well as the driver’s shift durations.

[9]:

pyvrp.plotting.plot_solution(res.best, m.data())

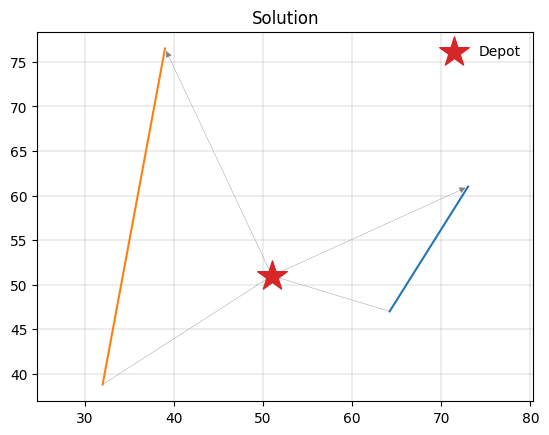
PyVRP supports many more time and duration constraints beyond time windows and shift durations. These include latest start constraints and overtime costs for vehicles, release times for client deliveries, service durations at clients and depots, and time windows for depots.

A business expansion¶

Both clients and drivers are happy with the routing decisions made using our updated model. Business is doing well, and a second depot location was recently opened to meet additional demand from new clients. The new depot initially has a single vehicle available. The company again approaches us, to help answer which clients should be serviced from each depot.

Luckily, PyVRP can easily solve routing problems with multiple depots. We simply extend the previous model with new data:

[10]:

NEW_COORDINATES = [(30, 80), (50, 90), (38.5, 82)]
NEW_DEMANDS = [5, 3, 7]
NEW_TIME_WINDOWS = [(0, 80), (0, 80), (80, 120)]

[11]:

# We extend the previous model with the new data.
new_depot = m.add_depot(x=40.0, y=70.0, name="New depot")
new_vehicles = m.add_vehicle_type(
    num_available=1,
    capacity=20,
    start_depot=new_depot,
    end_depot=new_depot,
    shift_duration=SHIFT_DURATION,
)

for idx in range(len(NEW_COORDINATES)):
    m.add_client(
        x=NEW_COORDINATES[idx][0],
        y=NEW_COORDINATES[idx][1],
        delivery=NEW_DEMANDS[idx],
        tw_early=NEW_TIME_WINDOWS[idx][0],
        tw_late=NEW_TIME_WINDOWS[idx][1],
        name=f"New client {idx + 1}",
    )

for frm in m.locations:
    for to in m.locations:
        dist = int(abs(frm.x - to.x) + abs(frm.y - to.y))
        m.add_edge(frm, to, distance=dist, duration=dist)

res = m.solve(stop=pyvrp.stop.MaxRuntime(1))  # one second of runtime

PyVRP v0.14.0a0

Solving an instance with:
    2 depots
    7 clients
    3 vehicles (2 vehicle types)

    Iters    Time |      Current OK    Candidate OK         Best OK

Search terminated in 1.00s after 24467 iterations.
Best-found solution has cost 214.

Solution results
================
    # routes: 3
     # trips: 3
   # clients: 7
   objective: 214
    distance: 214
    duration: 214
# iterations: 24467
    run-time: 1.00 seconds

PyVRP found a solution using three vehicles:

[12]:

for idx, route in enumerate(res.best.routes()):
    print(f"Route #{idx} [duration = {route.duration()}]:")

    for visit in route.schedule():
        loc = m.locations[visit.location]
        print(f" - [t = {visit.start_service:>03}] At {loc}.")

Route #0 [duration = 62]:
 - [t = 029] At Depot.
 - [t = 060] At Client 4.
 - [t = 091] At Depot.
Route #1 [duration = 71]:
 - [t = 006] At Depot.
 - [t = 038] At Client 3.
 - [t = 060] At Client 2.
 - [t = 077] At Depot.
Route #2 [duration = 81]:
 - [t = 012] At New depot.
 - [t = 019] At Client 1.
 - [t = 031] At New client 1.
 - [t = 061] At New client 2.
 - [t = 080] At New client 3.
 - [t = 093] At New depot.

Let’s have a look:

[13]:

pyvrp.plotting.plot_solution(res.best, m.data())

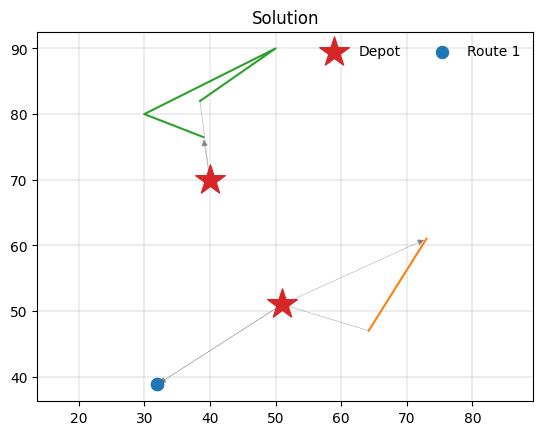
Additionally, PyVRP supports vehicles starting and ending their routes at different depots, as well as reloading along the route.

Conclusion¶

In this quickstart notebook we have solved the business case of a small delivery company. You have learned how to specify depots, vehicle types, and clients using PyVRP’s modelling interface, and learned how to model time and duration constraints, as well as multiple depots. With these fundamentals, you now have a solid grasp of modelling routing problems with PyVRP.